区块链深度学习系列|椭圆曲线数字签名发展史


Comunion 是一个去中心化的(DAO) 组织协作网络,提供面向数字时代的全新商业基础设施和价值转化机制,致力于让劳动价值 像 资本一样自由流通、交易和积累。
本系列内容包含: 基本概念及原理、密码学、共识算法、钱包及节点原理、挖矿原理及实现。
密码学有两类: 私钥密码学,公钥密码学 。也可以称之为: 对称密码学,非对称密码学 。
其中公钥密码里面有三个基本原理: 公钥加密、数字签名、密钥协商 。
本文详细阐述的内容是:现代密码学里面,公钥密码学中数字签名中的一种——椭圆曲线数字签名。椭圆曲线数字签名算法(ECDSA)是使用椭圆曲线对数字签名算法(DSA)的模拟。
学科为什么这样分类?数字签名是如何出现的?为什么产生?我们一起来了解一下密码学的发展历史。
私钥密码学
说起密码学,其实我们并不陌生,比如二战期间德国使用的加密机,在战争期间起到了很重要的作用。从那个时候就已经展现展示出了密码学的一些作用和用处。
当时二战期间德国使用的密码机是恩尼格玛密码机(德语Enigma,又译哑谜机,或谜)。这个密码机放到当前密码学学科里面,属于经典密码学。
经典密码学经典密码是一种密码类型,过去历史上常用,但现代大部分的已经不再使用了。经典密码是基于一个拼音字母(像是 A-Z)、动手操作或是简单的设备,以使用了很多的技巧而著称。
经典密码学也可能是一种简单的密码法,以致于其效率和安全性并不值得信赖。而我们现在所了解的新密码学被称之为现代密码学,也就是私钥密码学和公钥密码学。
既然现代密码学中分私钥密码学和公钥密码学,那么什么是私钥密码学呢?
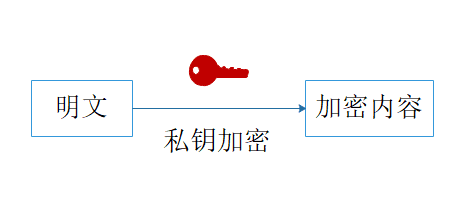
也就是当使用私钥密码学进行加密、解密的时候,使用的密钥是同一把。
例如,张三和李四进行通信,张三将一段明文加密,之后通过网络传播给李四,李四需要解密这段密文才能看到明文。那么在这个过程当中,张三进行加密的密钥和李四解密使用的密钥是相同的。
这里面存在一个很大的弊端,在这个传输过程中,李四获得密钥的方式有以下两种:
1.张三和李四私下见面,张三将密钥当面给李四;
2.张三将密钥直接在线发给李四。
第一种方式,由于只有两个人见面,所以其他人不会知道,这种方式很安全,但是很不方便,尤其是成本太大。比如一个人在中国,一个人在美国。这还是点对点,如果成千上万的人需要传输,那么这种方式根本不可行。
第二种方式,通过网络传送很方便,但是严格来说是不安全的,因为直接传送密钥的话,那么相当于传送的数据是明文,而其他人可以通过一些其他方法截获这些数据,所以存在很大的安全隐患。
在一个硕大的网络系统当中,如果使用私钥密码学,就会存在严重的问题,那就是密钥的共享问题,因为私钥密码学里面加密使用的密钥和解密使用的密钥是同一把。要么协商成本太大,要么存在风险。
这是私钥密码学和其存在的问题。科技永远是在不断的革新,有问题就要去解决,所以公钥密码学登上了历史舞台。
公钥密码学
在1976年,迪菲和赫尔曼两个人提出了一个具有划时代意义的思想,他们指出,在通信双方之间不直接传输加密密钥的保密通信是可能的。
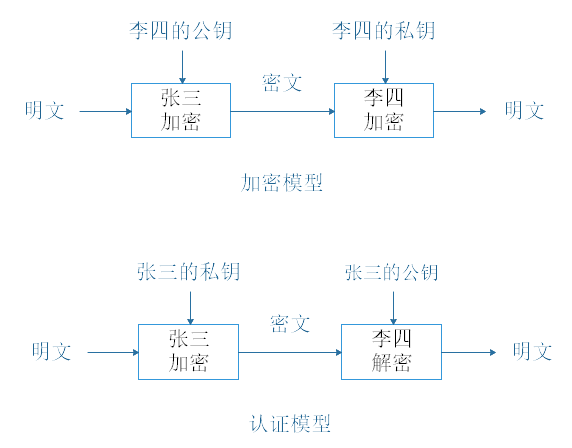
也就是把密钥分为加密的公钥和解密的私钥,当使用这个密钥对传输数据的时候,如果用公钥加密数据就必须用私钥解密,如果用私钥加密也必须用公钥解密,否则解密将不会成功。
这是第一个实用的在非保护信道中建立共享密钥方法,也可以简单理解为将张三加密的密钥和李四解密的密钥分成两把。
例如,张三和李四通过公钥加密算法得到一个唯一的密钥对(公钥和私钥),两人各持一把,比如张三持公钥,李四持私钥。张三要给李四传输秘密数据,那么张三通过公钥进行加密,只有持有李四的私钥才可以将信息进行解密。反之,李四通过私钥进行加密,只有持有张三的公钥才可以解密。
这样即使信息在传送过程中,即使被第三方截取,也不可能获取其中的内容。
如果在一个硕大的网络系统当中,所有人都将自己的公钥公开,保留自己的私钥。那么就解决了一个问题: 通信双方都有彼此公钥,通信时只要使用对方公钥进行加密并且传输数据,即便这些加密的密文是完全公开的,但是只有私钥持有人才能解密数据内容。
密钥协商
密钥协商是将上文提出的思想进行实现的过程,两人或多人即使没有任何关系,也可以通过公开的、不安全的通信网络进行交互,共同建立会话密钥,任何一个参与者均对结果产生影响,不需要任何可信的第三方。
其中会话密钥由每个协议参与者分别产生的参数通过一定的计算得出,这就是密钥协商协议。
密钥协商协会的生产方式可以分为两种: 证书型和证书型 。
证书型,是指在会话密钥的产生过程中,由一个可信的证书中心给参与密钥协商的各方主体分别发放一个证书,此证书中含有各方的公钥,ID及其他信息。优点是比较成熟,应用面广泛,公私钥均有利于统一管理。其缺点是强中心化,因此计算代价巨大,并且证书还需要维护。
无证书型,是指各方在进行会话密钥的协商过程中不需要证书的参与,不需要可信证的书中心参与,这样减少了计算量,同时安全性和证书型处于同一级别。其唯一缺点是设计起来比较复杂,因此现在无证书型是密钥协商协议的主流种类。
数字签名
数字签名是只有信息的发送者才能产生的别人无法伪造的一段数字串,这段数字串同时也是对信息的发送者发送信息真实性的一个有效证明。其作用是用来做数据认证的,它能够鉴定数据在网络当中传播是否被篡改。
每一种签名体制其实都根植于一个数学问题,当使用公钥加密完成之后,只有私钥拥有者才能解密,而其他人不能解密,其原理是基于数学问题的困难性。
我们通过代表性的公钥加密发展史来理解一下:
RSA_DSA,是基于整数分解问题设计的加密体制,这里的整数是很大的,比如是2^256长的比特串,此种加密体制没有涉及到数字签名。
ElGamal_DSA,是基于离散对数问题设计的加密体制。
EC_DSA,是基于有限运算的运算对数问题设计的加密体制。
Lattice_DSA,是基于最短象限的寻找问题设计的加密体制。
这四种加密体制出现的时间也是遵循从上到下的顺序,前三者在量子攻击面前是十分脆弱的,最后 Lattice_DSA 的出现就是为了抵御量子攻击,当然现阶段量子计算机从成熟到应用还有很长的一段时间。
数字签名和公钥的一些联系:签名者使用私钥进行签名,签名的私钥仅对自签名者公开,公钥是公开的,每个人都可以用公钥对私钥拥有者产生的签名进行验证,来验证是否是有私钥拥有者签署的。
有些朋友会问,在区块链系统系统当中,为什么主要使用的是椭圆曲线数字签名算法(ECDSA),而不是其它的呢?
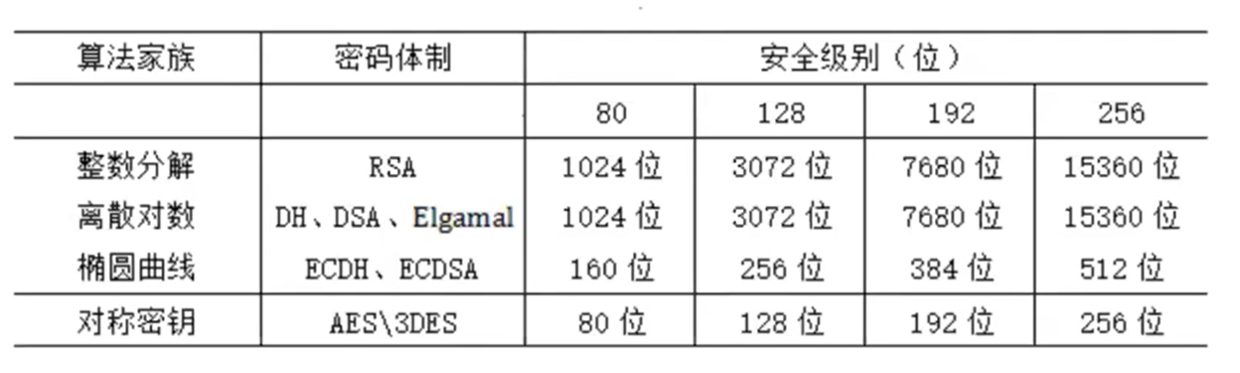
如上图所示,在椭圆曲线密码体制中,当私钥长度为160位比特长度的时候,其安全级别是80位(这里的80指的是2的80次方),当私钥长度为256位比特长度的时候,其安全级别是128位。
这里可以对比一下其他密码体制,比如 Elgamal 要想达到128位安全级别的话,其私钥长度是3072位,是椭圆曲线私钥长度的12倍。
而私钥的长度对密码体制的影响是: 私钥的长度越长,密码系统里面的加解密、签名、验签算法等,其效率越低。 因此,在同样的安全级别下,区块链系统使用了私钥更短、效率更高的椭圆曲线。
所以,之所以在区块链系统中主要使用的是椭圆曲线数字签名算法,主要是因为在数字签名算法中,椭圆曲线数字签名算法能够以相对较短的密钥长度达到更高的安全级别。

Cratos Leads Daily Surge as Fan Tokens and DeFi Assets Post Notable Gains
Cratos leads May 4 crypto rally with a 27% surge, as fan tokens and DeFi assets post double-digit ga...
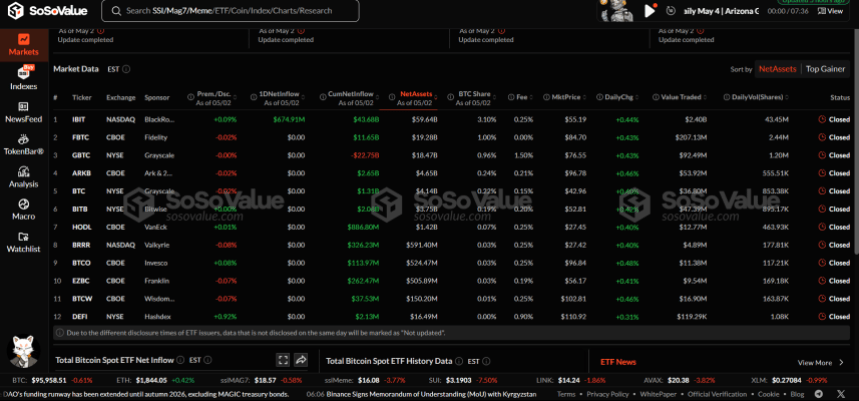
Bitcoin Spot ETFs Score $1.81 Billion In Net Inflows As Market Revival Continues
The US Bitcoin ETFs are strongly reflecting the bullish sentiments that are ravaging the crypto mark...

SUI and POL Investors Are Quietly Rotating Into Codename:Pepe — What’s Fueling This Shift?
The post SUI and POL Investors Are Quietly Rotating Into Codename:Pepe — What’s Fueling This Shift? ...