技术干货 | 理解零知识证明算法之Bulletproofs：Range Proof I

前言

Bulletproofs，又一个有意思的零知识证明算法，相信读者已经很熟悉它了。和zk-snark相比，它不需要可信设置；和zk-stark算法相比，它具有较小的proof size。根据论文，它有两个方面的应用：1. 用于range proof；2. 用于一般算术电路的零知识证明。下面，让我们先看一下Bulletproofs是如何高效的实现第一点。

Range proof

1. 预备知识

a _L ：表示向量{a ₁ ,a ₂ ……a _n }

2 ⁿ ：表示向量{2 ⁰ ,2 ¹ …2 ^n-1 }

<a, b>：表示向量内积 ∑ a _i *b _i ，结果是一个值

a o b：向量对应位相乘，{a ₁ *b ₁ ……a _n *b _n }，结果是一个向量

2. 证明

Alice想要证明 v ⸦ [0, 2 ⁿ -1]

=>则，需要证明一个relation得成立，如下所示：

{（ g 、 h ⸦ G ， V ， n ； v ， r ⸦ Z _p ）： V = g ^r h ^v ^ v ⸦ [0, 2 ⁿ -1] }

public-x           witness-w relation-R

即，对于公开信息x，Alice有隐私信息w，使得关系R成立。

令 a _L 为金额v的在范围[0, 2 ⁿ -1]内的二进制形式，则a _L = {a ₁ ,a ₂ ……a _n }⸦{0,1} ⁿ ，且满足<a _L , 2 ⁿ > = v。因此，证明者需要证明以下几个等式相等：

V = g ^r h ^v (1)

<a _L , 2 ⁿ > = v    (2)

a _L o a _R = 0 ⁿ (3)

a _R = a _L - 1 ⁿ (4)

等式(1)确保了承诺V和金额v的绑定关系，等式(2)确保了v的范围，等式(3)(4)确保了a _L 元素只属于{0,1}。等式(2)/(3)/(4)总共包含了2n+1个约束，其中公式(2)1个，公式(3)(4)各n个。接下来，为了效率，我们需要把2n+1个约束转换成1个约束。

3. 2n+1个约束转换成1个约束

=>预备：从Z _p 中任意选择一个数y，则b = 0 ⁿ 是等式<b, y ⁿ > = 0成立的充分条件；因为当b != 0 ⁿ ，等式成立的概率仅有n/p，p是有限域，远大于n。（理解：如果b != 0 ⁿ ，把等式看作求n阶一次多项式的零点即可）因此，如果有<b, y ⁿ > = 0，那么验证者愿意相信b != 0 ⁿ 。

利用这个理论，我们把等式(2)/(3)/(4)做以下转换：

1. 验证者随机选取一个数y发送给证明者；

2. 证明者要证明：

<a _L , 2 ⁿ > = v (5)

<a _L , a _R o y ⁿ > = 0        (6)

<a _L - 1 ⁿ - a _R , y ⁿ > = 0    (7)

同理，等式(5)确保了v的范围，等式(6)(7)确保了a _L 元素只属于{0,1}。此时2n+1个约束转换成3个约束，接下来，还需要做进一步的处理：

1. 验证者随机选取一个数z发送给证明者：

2. 证明者利用z对公式(5)(6)(7)进行线性组合，得到如下公式：

z ² * <a _L , 2 ⁿ > + z * <a _L - 1 ⁿ - a _R , y ⁿ > + <a _L , a _R o y ⁿ > = z ² * v    (8)

至此，我们已经把2n+1个约束转换成1个约束。下面我们对公式(8)做进一步的优化，把三个点积优化成1个点积

4. 三个点积优化成1个点积

=> z ² * <a _L , 2 ⁿ > + z *  <a _L - 1 ⁿ - a _R , y ⁿ > + <a _L , a _R o y ⁿ > = z ² * v

=> <a _L , z ² * 2 ⁿ > + <a _L , z * y ⁿ > - <z * 1 ⁿ , y ⁿ > - <z * a _R , y ⁿ > + <a _L , a _R o y ⁿ > = z ² * v

=> <a _L , a _R o y ⁿ + z * y ⁿ + z ² * 2 ⁿ > - <z * 1 ⁿ , y ⁿ > + <z * 1 ⁿ , y ⁿ o a _R > = z ² * v

=> <a _L , a _R o y ⁿ + z * 1 ⁿ o y ⁿ + z ² * 2 ⁿ > - <z * 1 ⁿ , y ⁿ + y ⁿ o a _R > = z ² * v

=> <a _L , (a _R + z * 1 ⁿ ) o y ⁿ + z ² * 2 ⁿ > -  <z * 1 ⁿ , y ⁿ + y ⁿ o a _R > = z ² * v

=> <a _L , (a _R + z * 1 ⁿ ) o y ⁿ + z ² * 2 ⁿ > -  <z * 1 ⁿ , (a _R + z * 1 ⁿ ) o y ⁿ + z ² * 2 ⁿ -z * 1 ⁿ * y ⁿ + y ⁿ - z ² *2 ⁿ >  =  z ² * v

=>  <a _L - z * 1 ⁿ , (a _R + z * 1 ⁿ ) o y ⁿ + z ² * 2 ⁿ > - <z * 1 ⁿ , -z * 1 ⁿ * y ⁿ + y ⁿ - z ² *2 ⁿ > =  z ² * v

=>  <a _L - z * 1 ⁿ , (a _R + z * 1 ⁿ ) o y ⁿ + z ² * 2 ⁿ > = z ² * v + <z * 1 ⁿ , -z * 1 ⁿ * y ⁿ + y ⁿ - z ² *2 ⁿ >

=>  <a _L - z * 1 ⁿ , (a _R + z * 1 ⁿ ) o y ⁿ + z ² * 2 ⁿ > = z ² * v + <z * 1 ⁿ , (-z * 1 ⁿ + 1 ⁿ ) * y ⁿ > - <z * 1 ⁿ ,  z ² *2 ⁿ >

=>  <a _L - z * 1 ⁿ , (a _R + z * 1 ⁿ ) o y ⁿ + z ² * 2 ⁿ > = z ² * v + (z – z ² ) * <1 ⁿ , y ⁿ > - z ³ * <1 ⁿ , 2 ⁿ >    (9)

=>  令

L =  a _L - z * 1 ⁿ

R =  (a _R + z * 1 ⁿ ) o y ⁿ + z ² * 2 ⁿ

δ =  (z – z ² ) * <1 ⁿ , y ⁿ > - z ³ * <1 ⁿ , 2 ⁿ >

5. 验证：

1. 证明者把L/R/V发送给验证者；

2. 验证者事先算好 δ

3. 验证者根据L算出来a _L ，根据<a _L , 2 ⁿ > = v算出v

4. 验证者根据L,R,v,δ验证等式<L, R> = z ² * v +δ

因为y，z都是验证者提供，因此如果验证者如果能验证公式(9)成立，则相信等式(5)(6)(7)成立，则相信等式(2)(3)(4)成立，则相信v满足关系v ⸦ [0, 2 ⁿ -1]。

但是，可以看到上述过程，泄露了v的信息，因此需要一个零知识证明协议。

6.  一个零知识证明协议

由于L,R包含了v的相关信息，因此，我们需要添加两个盲因子s _{L 、} s _R 来隐藏a _L ，a _R 。如公式(10)(11)所示：

l(X) = (a _L - z * 1 ⁿ ) + s _L * X )   (10)

r(X) = (a _R + z * 1 ⁿ + s _R * X) o y ⁿ + z ² * 2 ⁿ (11)

此时，定义公式(12)

t(X) = <l(X), r(X)> = t ₀ + t ₁ *X + t ₂ * X ² (12)

可以看出系数t ₀ 是l(x)和r(x)常数项的乘积，即满足：

t ₀ = <L, R> = z ² *v + δ

因此，问题由证明：

<L, R> = z ² *v + δ

转化成了，在任意一点x，验证者验证多项式值l(x), r(x), t(x)满足关系：

<l(x), r(x)> = t(x)

多项式值l(x), r(x), t(x)由证明者提供，为了保证l(x)，r(x) well-formed，即：

l(x) = (a _L - z * 1 ⁿ ) + s _L * x )

r(x) = (a _R + z * 1 ⁿ + s _R * x) o y ⁿ + z ² * 2 ⁿ

需要校验：

P = A * S ^x * g ^(-z) *(h`) ^{z*yn+z^2*2^n}

= h ^α g ^aL h ^aR * (h ^ρ g ^sL h ^sR ) ^x * g ^(-z) * (h`) ^{z*y^n+z^2*2^n}

= h ^α g ^aL h ^aR *  h ^{ρ x} g ^sL*x h ^sR*x * g ^(-z) * (h`) ^{z*y^n+z^2*2^n}

= h ^α+ρx * g ^{aL + sL * x – z * 1^n} * h ^{aR + sR * x} * (h`) ^{z*y^n+z^2*2^n}

= h ^α+ρx * g ^{aL + sL * x – z * 1^n} * (h`) <sup>y^n o (aR + sR * x)</sup> * (h`) ^{z*y^n+z^2*2^n}

= h ^α+ρx * g ^{aL + sL * x – z * 1^n} * (h`) ^{y^n o (aR + sR * x) + z*y^n+z^2*2^n}

= h ^α+ρx * g ^{aL + sL * x – z * 1^n} * (h`) ^{y^n o (aR + sR * x + z * 1^n) + z^2*2^n}

=? h ^μ g ^l (h`) ^r

=> 当且仅当 l /r well-formed ，等式成立

为了保证t(x) well-fromed，即：

t = t ₀ +t ₁ x + t ₂ x ²

需要校验：

=> g ^t h ^τx =? V ^{z^2} * g ^δ *T ₁ ^x *T ₂ ^{x^2}

=> g ^t h ^{τ x} =? (h ^r g ^v ) ^{z^2} *g ^δ *(g ^t1 ) ^x *(h ^τ1 ) ^x *(g ^t2 ) ^{x^2} *(h ^τ2 ) ^{x^2}

=> g ^t h ^{τ x} =? h ^{z^2*r + τ1*x + τ2*x^2} * g ^{z^2*v + δ + t1*x + t2*x^2}

=> g ^t h ^{τ x} =? h ^{z^2*r + τ1*x + τ2*x^2} * g ^{t0 + t1*x + t2*x^2}

=> t = ? t ₀ + t ₁ *x + t ₂ *x ² && τ _x = ? z ² *r + τ ₁ *x + τ ₂ *x ²

=> 当且仅当 t 和 τ _x welle-formed ，等式成立

具体的协议流程图如下图所示：

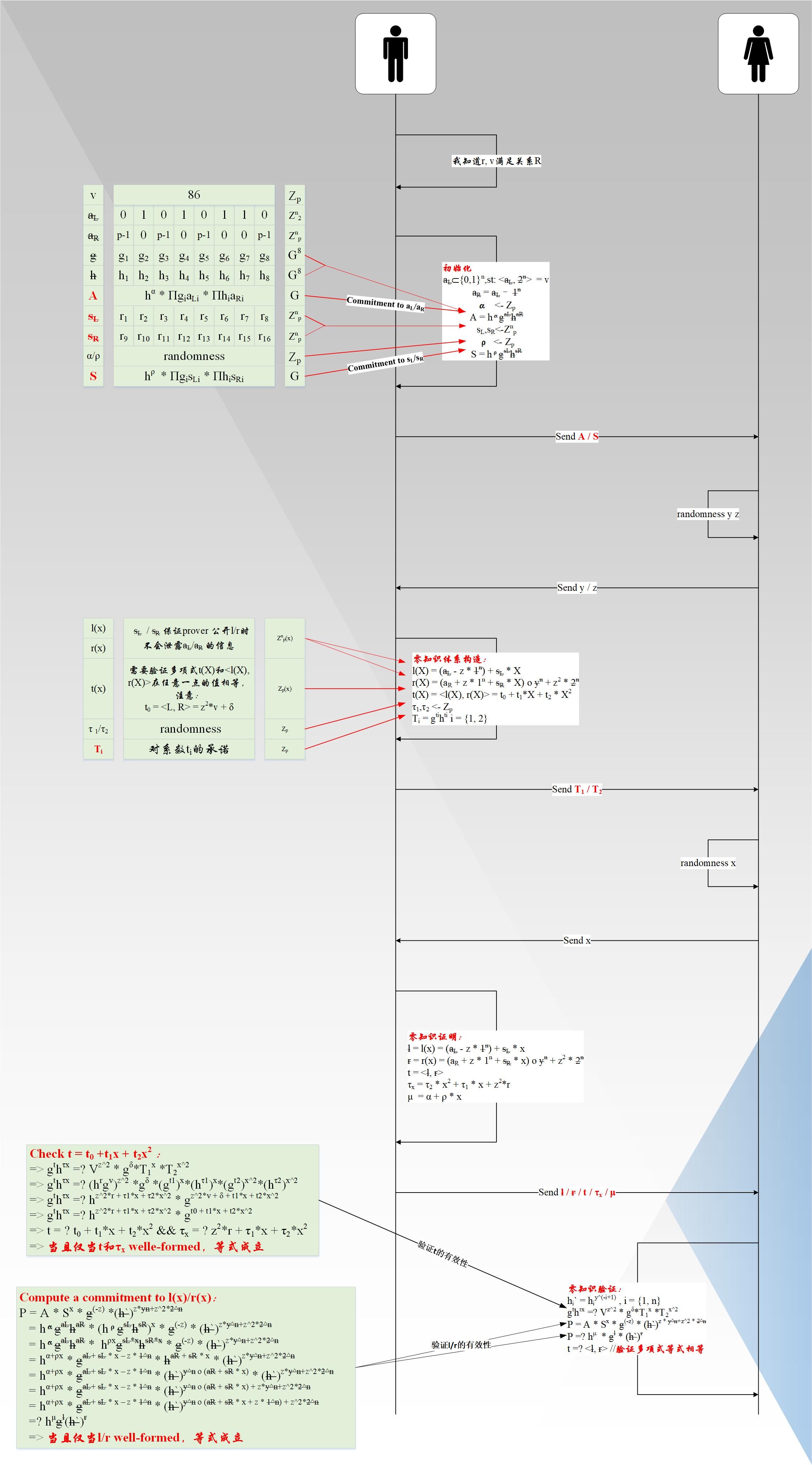
总结

从上述流程可以看出，一次range proof，证明者需要发送总共{ l / r / t / τ _x / μ / T ₁ / T ₂ / A / S }个元素给验证者，总共2n+3个Z _p 元素，4个G元素。下一篇文章将细讲，Bulletproofs如何将交互复杂度降低到对数级O(log(n))

附录

1. Bulletproofs 论文： chrome-extension://cdonnmffkdaoajfknoeeecmchibpmkmg/assets/pdf/web/viewer.html?file=https%3A%2F%2Feprint.iacr.org%2F2017%2F1066.pdf