引言:Gonka PoW 2.0的核心机制
Gonka PoW 2.0的核心思想是将传统的工作量证明转化为有意义的AI计算任务。本文将深入剖析其两大核心机制:计算挑战的生成与防作弊验证体系,展示这一创新共识机制如何在保证计算有用性的同时,建立可靠的防作弊保障体系。
整个流程可以概括为以下图示: 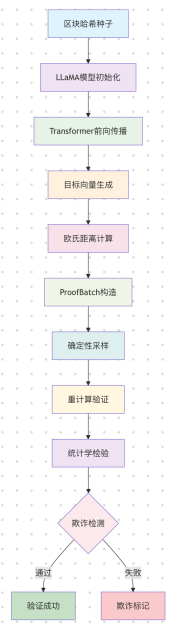
1. 计算挑战的生成机制
计算挑战是Gonka PoW 2.0的核心,它将传统的工作量证明转化为有意义的AI计算任务。与传统PoW不同,Gonka的计算挑战不是简单的哈希计算,而是一次完整的深度学习推理过程,既保证了网络安全,又产生了可用的计算结果。
1.1 种子系统的统一管理
所有计算过程都由统一的种子驱动,确保全网节点运行相同的计算任务。这种设计保证了计算的可重现性和公平性,每个节点都必须执行相同的计算任务才能获得有效的结果。
数据来源 :mlnode/packages/pow/src/pow/compute/compute.py#L217-L225

种子系统的关键要素包括:
- 区块哈希 :作为主种子,确保计算任务的一致性
- 公钥 :标识计算节点的身份
- 区块高度 :确保时间同步
- 参数配置 :控制模型架构和计算复杂度
1.2 LLaMA模型权重的确定性初始化
每个计算任务都从统一的LLaMA模型架构开始,通过区块哈希确定性初始化权重。这种设计确保了所有节点使用相同的模型结构和初始权重,从而保证计算结果的一致性。
数据来源 :mlnode/packages/pow/src/pow/models/llama31.py#L32-L51 

权重初始化的数学原理:
- 正态分布 :N(0, 0.02²) - 小方差确保梯度稳定性
- 确定性 :相同区块哈希产生相同权重
- 内存效率 :支持float16精度以减少显存占用
1.3 目标向量生成与距离计算
目标向量在高维单位球面上均匀分布,这是计算挑战公平性的关键。通过在高维空间中生成均匀分布的目标向量,确保了计算挑战的随机性和公平性。
数据来源 :mlnode/packages/pow/src/pow/random.py#L165-L177 
在4096维的词汇表空间中,球面几何具有以下特性:
- 单位长度 : 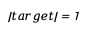
- 角度分布 :任意两个随机向量的夹角趋向于90°
- 集中现象 :大部分质量分布在球面表面附近
球面均匀分布的数学原理:
在n维空间中,单位球面上的均匀分布可以通过以下方式生成:
1. 首先生成n个独立的标准正态分布随机变量: 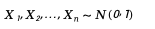
2. 然后进行归一化: 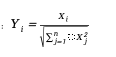
这种方法确保了生成的向量在球面上均匀分布,数学表达式为:
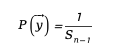
其中 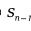 是n-1维球面的表面积。
是n-1维球面的表面积。
距离计算是验证计算结果的关键步骤,通过计算模型输出与目标向量的欧氏距离来衡量计算的有效性:
数据来源 :基于mlnode/packages/pow/src/pow/compute/compute.py中的处理逻辑 


距离计算的步骤:
1. 排列应用 :按照排列种子重排输出维度
2. 向量归一化 :确保所有输出向量位于单位球面上
3. 距离计算 :计算与目标向量的欧氏距离
4. 批次封装 :将结果封装为ProofBatch数据结构
2. 防作弊验证机制
为了确保计算挑战的公平性和安全性,系统设计了精密的防作弊验证体系。这一机制通过确定性采样和统计学检验来验证计算的真实性,防止恶意节点通过作弊获得不当收益。
2.1 ProofBatch数据结构
计算结果被封装为ProofBatch数据结构,这是验证流程的核心载体。ProofBatch包含了计算节点的身份信息、时间戳以及计算结果,为后续的验证提供了必要的数据基础。
数据来源 :mlnode/packages/pow/src/pow/data.py#L8-L25 

ProofBatch数据结构的特性:
- 身份标识 :public_key唯一标识计算节点
- 区块链绑定 :block_hash和block_height确保时间同步
- 计算结果 :nonces和dist记录所有尝试及其距离值
- 子批次支持 :支持提取满足阈值的成功计算
2.2 确定性采样机制
为了提高验证效率,系统采用了确定性采样机制,只验证部分计算结果而非全部。这种设计既保证了验证的有效性,又大大降低了验证成本。
Gonka的验证采样率通过链上参数统一管理,确保全网一致性:
数据来源 :inference-chain/proto/inference/inference/params.proto#L75-L78

数据来源 :inference-chain/x/inference/types/params.go#L129-L133

基于种子系统,采样过程完全确定性,确保验证的公平性。通过使用SHA-256哈希函数和验证者的公钥、区块哈希、区块高度等信息生成种子,确保所有验证者使用相同的采样策略:
数据来源 :decentralized-api/mlnodeclient/poc.go#L175-L201 
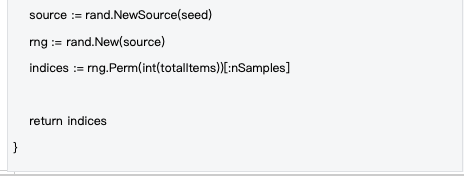

确定性采样的优势:
- 公平性 :所有验证者使用相同的采样策略
- 效率 :只验证部分数据,降低验证成本
- 安全性 :难以预测被采样的数据,防止作弊
2.3 统计学欺诈检测
系统使用二项分布检验来检测欺诈行为,通过统计学方法判断计算节点是否诚实。这种方法基于硬件精度和计算复杂度设定了预期的错误率,并通过统计检验来检测异常。
数据来源 :mlnode/packages/pow/src/pow/data.py#L7 
预期错误率的设定考虑了以下因素:
- 浮点精度 :不同硬件的浮点运算精度差异
- 并行计算 :GPU并行化导致的数值累积误差
- 随机性 :模型权重初始化的微小差异
- 系统差异 :不同操作系统和驱动的计算行为差异
数据来源 :mlnode/packages/pow/src/pow/data.py#L174-L204




总结:构建安全可靠的AI计算网络
Gonka PoW 2.0通过精心设计的计算挑战和防作弊验证机制,成功地将区块链的安全需求与AI计算的实际价值相结合。计算挑战确保了工作的意义性,而防作弊机制则保障了网络的公平性和安全性。
这种设计不仅验证了"有意义挖矿"的技术可行性,更为分布式AI计算建立了新的标准:计算必须既安全又有用,既可验证又高效。
通过将统计学、密码学和分布式系统设计相结合,Gonka PoW 2.0成功地在保证计算有用性的同时,建立了可靠的防作弊机制,为"有意义挖矿"的技术路线提供了坚实的安全基础。
注:本文基于Gonka项目的实际代码实现和设计文档编写,所有技术分析和配置参数均来自项目官方代码库。
关于 Gonka.ai
Gonka 是一个旨在提供高效 AI 算力的去中心化网络,其设计目标是最大限度地利用全球 GPU 算力,完成有意义的 AI 工作负载。通过消除中心化守门人,Gonka 为开发者和研究人员提供了无需许可的算力资源访问,同时通过其原生代币 GNK 奖励所有参与者。
Gonka 由美国 AI 开发商 Product Science Inc. 孵化。该公司由 Web 2 行业资深人士、前 Snap Inc. 核心产品总监 Libermans 兄妹创立,并于 2023 年成功融资 1800 万美元,投资者包括 OpenAI 投资方 Coatue Management、Solana 投资方 Slow Ventures、K 5、Insight and Benchmark 合伙人等。项目的早期贡献者包括 6 blocks、Hard Yaka、Gcore 和 Bitfury 等 Web 2-Web 3 领域的知名领军企业。
官网 | Github | X | Discord | 白皮书 | 经济模型 | 用户手册